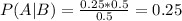Question

Consider two hard disks, d1, and d2, such that in 50,000 hours of operation d1 fails with probability 1/3 and d2 fails with probability 1/4 (independent of each other). Suppose that we pick uniformly at random one of the two disks to use in a data server. What is the probability that we picked d2 for the server given that there was a disk failure during the 50,000 hours of server operation? Explain your answer.

Hint: Use the Bayes formula. The problem is similar to the biased die example presented in class.

Answer 1

0.25

Explanation:

Let A be the event that we pick d2, and B is the event that the disk failure during 50000 hours operation

According to Bayes formula theorem, the probability that the disk d2 given that there was a disk failure during the 50000 hours of server operation:

`P(A|B) = (P(B|A) * P(A))/(P(B))`

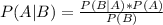
Where P(B|A) is the probability that the disk would fail during the 50000 hours operation given that it's d2, which is 1/4.

P(A) is the probability that d2 is pick, which is 0.5 since we pick uniformly.

P(B) is the probability that (any) disk fails during 50000 hours operation. We can calculate by first calculate the probability that no disk would fail, which is

`(1 - (1)/(3))(1 - (1)/(4)) = (2)/(3)(3)/(4) = (1)/(2)`

Then we can subtract this from 1 to find P(B) = 1 - 1/2 = 1/2

Therefore,

`P(A|B) = (0.25 * 0.5)/(0.5) = 0.25`