Question

A policyholder wishes to annuitize the cash value of her insurance policy at retirement. She desires an annual payment of $95,000 per year and the cash value is expected to be $1,100,000 at retirement. Approximately how many payments can she expect to receive if annuity interest rates are 5.122 percent

Answer 1

Answer: 18 years

Explanation: The formula for calculating the number of periods is

n = log (
`1-(PV(r))/(P) ^(-1)`) / Log (1+r)

PV = $1,100,000

P = 95,000

r = 0.05122

log is the natural logarithm (you will find it on your calculator as log or on Excel as LN( )

n = log (
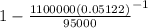`1-(1100000(0.05122))/(95000) ^(-1)`) / Log (1+0.05122)

= log (
`1-(56342)/(95000) ^(-1)`) / log (1.05122)

= log (
`(1 - 0.59307)^(-1)`) / log (1.05122)

= log
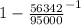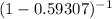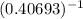`(0.40693)^(-1)` / log (1.05122)

= log 2.4574 / log (1.05122)

= 17.99 years

Approximately 18 years