Answer:
The mean of his total score if the golfer plays a full 18 holes is 172 and standard deviation is 11.3
Step-by-step explanation:
Given data:
For the first nine holes:
- Mean Score = 86
- Standard Deviation = 8
For the second nine holes:
- Mean Score = 86
- Standard Deviation = 8
We know that
For the two independent numbers A and B, the sum of mean of these numbers is equal to the mean of a number C.
Mean of A + Mean of B = Mean of C
Applying this to our situation, we get:
Mean for 1st half 9 holes + Mean for 2nd half 9 holes = Mean for full 18 holes
Rearranging the above equation
Mean of score for full 18 holes = Mean of score for 1st half 9 holes + Mean of score for 2nd half 9 holes
Putting the values of mean in above equation we get,
Mean of score full 18 holes = 86 + 86
Mean of score full 18 holes = 172
Now for standard deviation, the same property applies,
For the two independent numbers A and B, the sum of standard deviation these numbers is equal to the standard deviation of a number C.
Standard deviation of C =
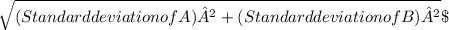
Applying this to our situation and replacing Standard deviation with SD,
SD of score for full holes =
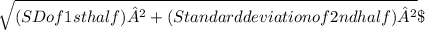
SD of score for full holes =
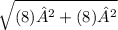
SD of score for full holes =
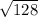
SD of score for full holes = 11.3