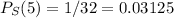Question

Streaks. In this problem we consider the problem of testing whether a randomly generated sequence is truly random. A certain computer program is supposed to generate Bernoulli iid sequences with parameter 0.5. When you try it out, you are surprised that it contains long streaks of 1s. In particular, you generate a sequence of length 200, which turns out to contain a sequence of 8 ones in a row. a. Let S be equal to the longest streak of 1s in an iid Bernoulli sequence of length 5. Compute the pmf of S exactly.

Answer 1

`P_S(0) = 1/32`

`P_S(1) = 12/32`

`P_S(2) = 11/32`

`P_S(3) = 5/32`

`P_S(4) = 2/32`

`P_S(5) = 1/32`

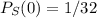
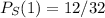
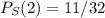
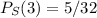
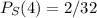
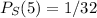
Explanation:

Let X be a sequence of iid Bernoulli with paramenter 0.5. X has Binomial distribution with parameters n = 5, p = 0.5.

S will be 0 only if your sequence of length 5 has only 0s, thus

`P_S(0) = P_X(0) = (1-0.5)⁵ = 0.5⁵ = 1/32 = 0.03125`

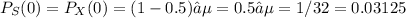
Note that each configuration of the list is one equally probable case out of 32.

S will be 1 only when X doesnt take the value 1 two times in a row. X can take the value 1 only once, which are 5 total cases out of 32, it can take the value 1 on the first element and the third/ fourth/fifth, the value 1 on the second element and the fourth/fifth, the value 1 on the third and fifth element or the value 1 on the first, third and fifth element. In total, we have 12 favourable cases from a total of 32, hence

`P_S(1) = 12/32 = 0.375`

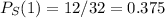
S will take the value 2 if any 2 consecutive values are 1 and the rest 0. Lets divide in cases:

• If the first two values are 1, then the third should be 0, and the fourth/fifth can be anything. So we have 4 possibilities.
• If the first value is 0, and the second and third are 1, the fourth should also be 0 and the fifth can be anything, we have 2 options.
• If the third and fourth value are 1, then, the second and fifth value must be 0, but the first one can be anything, so we have 2 possibilities.
• If the fourth and fifth value are 1, the third should be 0, and the first two can be anything. We have 3 new possibilities, because we alredy counted the case in which the first two elements are 1.

As a conclusion
`P_S(2) = 4+2+2+3/32 = 11/32 = 0.34375`

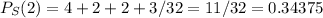
For S to be equal to 3 we have 5 possibilities: the first 3 elements are 1, the fourth is 0 and the fifth is either 1 or 0, the last 3 elements are 1, the second is 0 and the first one is either 1 or 0, or the first and fifth elements are 0 and the rest 1. Therefore,
`P_S(3) = 5/32 = 0.15625`

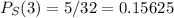
S is 4 only in 2 possible cases (an extreme is 0, and the rest is 1). So
`P_S(4) = 2/32 = 0.0625`

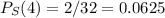
There is only one favourable case for 5, so
`P_S(5) = 1/32 = 0.03125`