Answer:
Two irrational numbers such that when you add them gives you a rational number could be
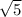 and
and
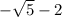 .
.
The result when adding these is -2 which is a rational number.
(There are infinitely many examples.)
Explanation:
How about opposite irrational numbers?
The sum of opposite numbers, no matter the classification of that number, is 0.
So examples:
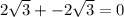
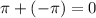
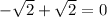
If you wanted some more examples that have a sum other than 0:
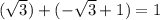
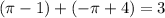
There are infinite amount of examples of the sum of two irrational numbers being a rational.
My last example: Two irrational numbers such that when you add them gives you a rational number could be
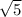 and
and
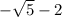 .
.
The result when adding these is -2 which is a rational number.