Answer:
The product of the two matrices is:
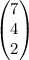
Explanation:
Matrix multiplication is not done element wise.
Two matrices 'A' and 'B' are said be compatible to multiplication iff A is of the size
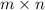 and B is of the size
and B is of the size
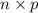 .
.
The product AB would be of the size
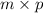 .
.
Here, the size of the first matrix is
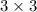 . Second matrix is
. Second matrix is
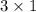 . Therefore, the resultant matrix would be:
. Therefore, the resultant matrix would be:
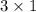 .
.
Now,
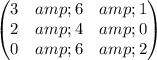
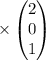
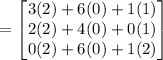

Therefore, the product is:
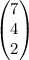 .
.