Answer: OPTION B.
Explanation:
We have the following functions f(x) and g(x):

In order to find for which values of "x"
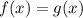 , we can check each option given:
, we can check each option given:
OPTION A
Substitute
 into the function f(x) and evaluate:
into the function f(x) and evaluate:
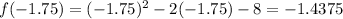
Substitute
 into the function g(x) and evaluate:
into the function g(x) and evaluate:
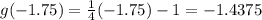
Substitute
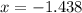 into the function f(x) and evaluate:
into the function f(x) and evaluate:
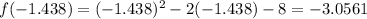
Substitute
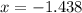 into the function g(x) and evaluate:
into the function g(x) and evaluate:
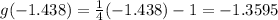
This is not the correct option.
OPTION B
We already know that:
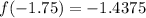
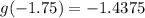
Substitute
 into the function f(x) and evaluate:
into the function f(x) and evaluate:
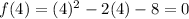
Substitute
 into the function g(x) and evaluate:
into the function g(x) and evaluate:
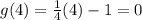
This is the correct option.
OPTION C
We already know that:

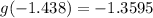
Therefore, this is not the correct option.
OPTION D
We already know that:
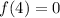
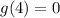
Substitute
 into the function f(x) and evaluate:
into the function f(x) and evaluate:

Substitute
 into the function g(x) and evaluate:
into the function g(x) and evaluate:
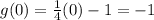
This is not the correct option.