Answer:
b. Do not reject the null hypothesis
Explanation:
Given that two random samples of 40 students were drawn independently from two populations of students. Assuming equal variances
we have the following data.
Sample 1
Mean:
76
Standard deviation:
8
Sample size:
40
Sample 2
Mean:
73
Standard deviation:
7
Sample size:
40
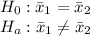
Difference -3.000
Standard error 1.681
95% CI -6.3462 to 0.3462
t-statistic -1.785
DF 78
Significance level P = 0.0782
Since p value >0.05,
b. Do not reject the null hypothesis