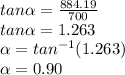Question

A resistor and capacitor are connected in series across an ac generator. The voltage of the generator is given by V ( t ) = V 0 cos ( ω t ) , where V 0 = 120 V , ω = 120 π rad / s , R = 700 Ω , and C = 3 μ F . (a) What is the magnitude of the impedance of the R C circuit? (b) What is the amplitude of the current through the resistor? (c) What is the phase difference between the voltage and current?

Answer 1

a) 1127.7ohms

b) 0.1714A

C) 0.90°

Step-by-step explanation:

From the AC Circuit where resistor and capacitor are arrange in series

Z=√(R)²+(XC)², Where R= resistor, Xc= Capacitance, also Xc=1/Wc

Therefore Xc= 1/120π×3×10⁻6, ∴ Xc= 884.19

Using Resistor R= 700ohms

Impedance Z= √(700)²+(884.19)² = 1127.7ohms

b) Using V=IR, and Voltage V= 120V

Hence Current I=V/R= 120/700= 0.1714A

c) The phase angle is express as TanФ=Xc/R =884.19/700= 1.263

Ф=Tan⁻⁽1.263⁾ =0.90°

Answer 2

a.1127.7Ω

b.0.1714A

c.
`0.9^(0)`

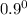
Step-by-step explanation:

From our knowledge of AC Circuit, where we have the resistor arranges in series with the capacitor, the total impedance(Z) of the circuit is given as

`Z=\sqrt{R^(2)+X_(C) ^(2)}\\`

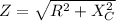
Where R is the resistor value in the circuit and
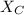`X_(C)` is the circuit capacitance due to the capacitor in the circuit and is express as

`X_(C)=(1)/(WC)\\`

By inserting values, we can determine the value of the capacitance

`X_(C)=(1)/(120\pi *3*10^(-6))\\X_(C)=884.19\\`

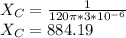
since the resistor value is 700Ω, we can substitute into the equation for the impedance

`Z=\sqrt{700^(2)+884.19 ^(2)}\\Z=1127.7ohms\\`

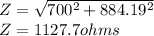
b. from the expression of Ohms law,
`V=IR`

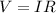
the voltage in this case is the amplitude of the voltage in the question i.e 120v

Hence
`I_(R)=120/700\\ I_(R)=0.1714A\\`

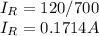
C. the phasor angle is express as

`tan\alpha=(X_(C) )/(R)`

`tan\alpha=(884.19 )/(700)\\tan\alpha=1.263\\\alpha=tan^(-1)(1.263)\\\alpha =0.90\\`