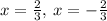Question

What are the two zeros of the quadratic function defined by the expression 9x{2}-4

Answer 1

The two zeros of the quadratic function are:

`x=(2)/(3),\:x=-(2)/(3)`

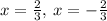
Explanation:

Given the expression

`9x^2-4`

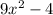
In order to determine the zeros of the quadratic function, we get the equation

`9x^2-4=0`

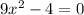
Add 4 to both sides

`9x^2-4+4=0+4`

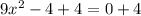
Simplify

`9x^2=4`

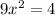
Divide both sides by 9

`(9x^2)/(9)=(4)/(9)`

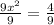
Simplify

`x^2=(4)/(9)`

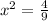
For x² = f(a) the solutions are:
`x=√(f\left(a\right)),\:\:-√(f\left(a\right))`

`x=\sqrt{(4)/(9)},\:x=-\sqrt{(4)/(9)}`

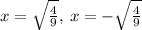
solving

`x=\sqrt{(4)/(9)}`

`=(√(4))/(√(9))`

`=(2)/(3)`

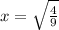
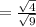
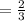
also solving

`x=-\sqrt{(4)/(9)}`

`=-(√(4))/(√(9))`

`=-(2)/(3)`

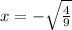
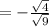
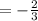
Therefore, the two zeros of the quadratic function are:

`x=(2)/(3),\:x=-(2)/(3)`