Question

(a) Calculate the magnitude of the acceleration due to gravity on the surface of Earth due to the Moon. (b) Calculate the magnitude of the acceleration due to gravity at Earth due to the Sun. (c) Take the ratio of the Moon's acceleration to the Sun's and comment on why the tides are predominantly due to the Moon in spite of this number.

Answer 1

`3.32* 10^(-5)\ m/s^2`

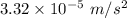
0.00061441 m/s²

0.05403

Step-by-step explanation:

G = Gravitational constant = 6.67 × 10⁻¹¹ m³/kgs²

Mass of Sun =
`1.989* 10^(30)\ kg`

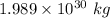
Mass of Earth =
`7.35* 10^(22)\ kg`

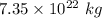
Distance between Earth and Moon = 384400000 m

Distance between Earth and Sun =
`147.3* 10^(9)\ m`

The acceleration due to gravity due to the moon is

`a_m=(GM)/(r^2)\\\Rightarrow a_m=(6.67* 10^(-11)* 7.35* 10^(22))/((384400000)^2)\\\Rightarrow a_m=3.32* 10^(-5)\ m/s^2`

The acceleration due to gravity due to the moon is
`3.32* 10^(-5)\ m/s^2`

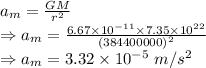
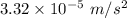
The acceleration due to gravity due to the Sun is

`a_s=(GM)/(r^2)\\\Rightarrow a_s=(6.67* 10^(-11)* 1.989* 10^(30))/((147.3* 10^(9))^2)\\\Rightarrow a_s=0.00061441\ m/s^2`

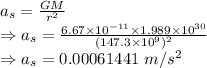
The acceleration due to gravity due to the Sun is 0.00061441 m/s²

`(a_m)/(a_s)=(3.32* 10^(-5))/(0.00061441)\\\Rightarrow (a_m)/(a_s)=0.05403\\\Rightarrow a_m=0.05403a_s`

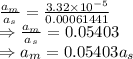
The moon's gravitational acceleration is 0.05403 times the sun's acceleration. However, tides are caused due to the bulging of the Earth's water towards the moon hence the moon is mostly responsible for the tides on Earth.