Note: Maybe you either forgot to mention the slope or forgot to mention another point from which the equation of the line passes.
In the later part, I would assume the slope m = 2 as an example.
Answer:
Please check the explanation.
Explanation:
Given
The point-slope form:
The point-slope form of the line equation is defined as
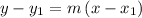
where
- m is the slope of the line
In our case:
(x₁, y₁) = (-4, -2)
substituting the point (-4, -2) in the point-slope form of the equation of the line
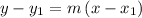
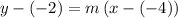
Therefore, the point-slope form of the equation of the line using the point (-4,-2) will be:
BONUS!
Example Solving with assuming the slope m = 2
Let suppose the slope m = 2
As we have already got the equation in the point-slope form
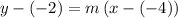
substituting m = 2
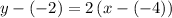
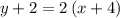
Subtract 2 from both sides

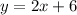
Thus, the point-slope form of the equation of the line using the point (-4,-2) and having slope m = 2.