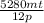Question

A solid yellow stripe is to be painted in the middle of a certain highway. If 1 gallon of paint covers an area of p square feet of highway, how many gallons of paint will be needed to paint a stripe t inches wide on a stretch of highway m miles long? (1 mile = 5,280 feet and 1 foot = 12 inches) \small \frac{5,280mt}{12p} \small \frac{5,280pt}{12m} \small \frac{5,280pmt}{12} \small \frac{(5,280)(12m)}{pt} \small \frac{(5,280)(12p)}{mt} Next Previous HelpEnd Review Review Screen

Answer 1

A solid yellow stripe is to be painted in the middle of a certain highway. If 1 gallon of paint covers an area of p square feet of highway, how many gallons of paint will be needed to paint a stripe t inches wide on a stretch of highway m miles long? (1 mile = 5,280 feet and 1 foot = 12 inches) \small \frac{5,280mt}{12p} \small \frac{5,280pt}{12m} \small \frac{5,280pmt}{12} \small \frac{(5,280)(12m)}{pt} \small \frac{(5,280)(12p)}{mt} Next Previous HelpEnd Review Review Screen

Step-by-step explanation:

Answer 2

`(5280mt)/(12p)`

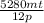
Step-by-step explanation:

Given,

Length of the highway = m miles = 5280m feet ( ∵ 1 mile = 5280 ft ),

It width = t inches =
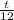`(t)/(12)` feet ( ∵ 1 feet = 12 inches ⇒ 1 inch = 1/12 feet )

Thus, the area of the highway,

`A=length* width`

`=5280m* (t)/(12)`

`=(5280mt)/(12)\text{ square feet}`

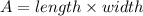
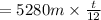
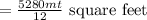
Since,

Paint required for p ft² area = 1 gallon,

Paint required for 1 ft² area = 1/p gallon,

∴ Paint required for
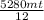`(5280mt)/(12)` ft² area =
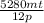`(5280mt)/(12p)` gallon,

Hence, the number of gallon of paint required is
`(5280mt)/(12p)`