Question

A certain model of automobile has its gas mileage (in miles per gallon, or mpg) normally distributed, with a mean of 32 mpg and a standard deviation of 4 mpg. Find the probability that a car selected at random has the following gas mileages.

Answer 1

The probability that a car selected at random has

(a) less than 26 mpg is 0.0668

(b) greater than 34 mpg is 0.3085

(c) between 30 and 34 mpg is 0.383

Explanation:

The question is missing, complete question is below:

A certain model of automobile has its gas mileage (in miles per gallon, or mpg) normally distributed, with a mean of 32 mpg and a standard deviation of 4 mpg. Find the probability that a car selected at random has the following gas mileages.

(a) less than 26 mpg (b) greater than 34 mpg (c) between 30 and 34 mpg

z-score of a specific value in the distribution of gas mileages can be found using:

z=
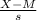`(X-M)/(s)` where

• X is the specific value

• M is the mean gas mileage in mpg (32 mpg)

• s is the standard deviation of the distribution (4 mpg)

Then

a) P(X<26) = P(z<z*) where

z*=
`(26-32)/(4)`=-1.5

P(z<z*) = 0.0668

b) P(X>34)=1-P(x<34)=1-P(z<z*) where

z*=
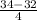`(34-32)/(4)`=0.5

Then 1-P(z<z*) = 1-0.6915 = 0.3085

c) P(30<X<34) =P(X<34)-P(X<30)

P(X<30)=P(z<z*) where

z*=
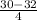`(30-32)/(4)`=-0.5

Then P(z<z*)=0.3085 Since P(X<34)=0.6915 we have

P(30<X<34) =0.6915-0.3085 =0.383