Question

Dole Pineapple Inc. is concerned that the 16-ounce can of sliced pineapple is being overfilled. Assume the standard deviation of the process is 0.03 ounce. The quality-control department took a random sample of 50 cans and found that the arithmetic mean weight was 16.05 ounces. At the 5% level of significance, can we conclude that the mean weight is greater than 16 ounces? What is the decision rule?

Answer 1

Answer: We concluded that the mean weight is greater than 16 ounces.

Explanation:

Since we have given that

n = 50

mean = 16.05 ounces

Standard deviation = 0.03 ounce

So, hypothesis:

`\mu =16\ ounces\\\\\mu>16\ ounces`

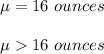
So, test statistic value would be

`z=\frac{\bar{x}-\mu}{(\sigma)/(√(n))}\\\\z=(16.05-16)/((0.03)/(√(50)))\\\\z=11.785`

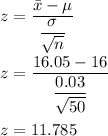
At 5% level of significance, z = 1.645 in one tail test.

Since 1.645 < 11.785

Hence, we will reject the null hypothesis.

Therefore, we concluded that the mean weight is greater than 16 ounces.