Answer:
a) z = 1.40
b) X is greater than or equal to 4.9
Explanation:
Population mean (μ) = 1.54
Standard deviation (σ) = 2.40
The z-score for any given value X is:
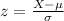
a) For X= 4.9:
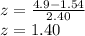
The corresponding z-score for x = 4.9 is z=1.40
b) Z-scores higher than 1.40 correspond to values of X higher than 4.9. Therefore, the area under the standard normal probability density function from z to infinity, P(z ≥ 1.40), is interpreted as the probability that X is greater than or equal to 4.9.