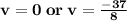Answer:
Solving the quadratic equation
 we get:
we get:
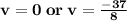
Explanation:
We need to solve the quadratic equation:

We can solve the quadratic equation of form
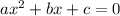 using quadratic formula:
using quadratic formula:
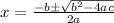
We need to put values of a , b and c in order to find the solutions of quadratic equations.
In the given equation:
 we have, a =8, b=37, c=0
we have, a =8, b=37, c=0
Putting values and finding the values for n:
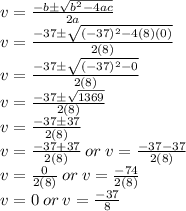
So, solving the quadratic equation
 we get:
we get: