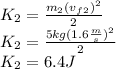Question

A 10-g bullet moving horizontally with a speed of 1.8 km/s strikes and passes through a 5.0-kg block initially at rest on a horizontal frictionless surface. The bullet emerges from the block with a speed of 1.0 km/s. What is the kinetic energy of the block immediately after the bullet emerges

Answer 1

`K_2=6.4J`

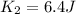
Step-by-step explanation:

According to the principle of conservation of momentum, we have:

`\Delta p=0\\p_i=p_f\\m_1v_1_i +m_2v_2_i=m_1v_1_f+m_2v_2_f`

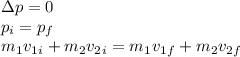
Here 1 is for the bullet and 2 is for the block. Since the block is initially at rest
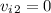`v_i_2=0`. Solving for
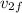`v_2_f` and replacing the given values:

`v_2_f=(m_1(v_1_i-v_1_f))/(m_2)\\v_2_f=(10*10^(-3)kg(1.8(km)/(s)-1(km)/(s)))/(5kg)\\v_2_f=0.0016(km)/(s)*(1000m)/(1km)=1.6(m)/(s)`

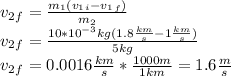
The kinetic energy of the block is given by:

`K_2=(m_2(v_f_2)^2)/(2)\\K_2=(5kg(1.6(m)/(s))^2)/(2)\\K_2=6.4J`