Question

A uniform horizontal strut weighs 400.0 N. One end of the strut is attached to a hinged support at the wall, and the other end of the strut is attached to a sign that weighs 200.0 N. The strut is also supported by a cable attached between the end of the strut and the wall. Assuming that the entire weight of the sign is attached at the very end of the strut, find the tension in the cable and the force at the hinge of the strut

Answer 1

Tension
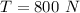`T=800\ N` upwards

Force
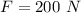`F=200\ N` downward

Step-by-step explanation:

Since the weight of the strut is uniform therefore it can be considered as a uniformly distributed load of 400
`N.m^(-1)` over a mass-less beam.

According to the given conditions one end of the strut is attached to a hinge and the other is loaded with a sign of 200 N and supported by a cable in the middle of the span of strut as shown in the schematic.

Now, for the equilibrium condition:

Forces are balanced:

`\sum F_x=0`

`\sum F_y=0`

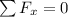
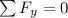
i.e.

`T+F=200+400`

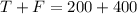
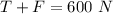`T+F=600\ N` .....................(1)

Moment about any point is balanced:

`\sum M=0`

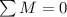
Taking moment about the hinge point:

`F* 0+(T-400)* (x)/(2) = 200* x`

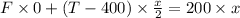
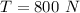`T=800\ N` upwards

Now put this value in eq. (1)

`F=-200\ N`

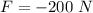
i.e. negative sign denotes opposite direction to the presumed one.

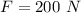`F=200\ N` downward