Question

each statement below describes the transformation of the graph f(x)=x square. which statement correctly describes the graph of g(x)=(x-7)^2 +7

Answer 1

The correct option is:

The graph of g(x) is the graph of f(x) translated 7 units up and 7 units right.

Option A is correct option.

Explanation:

The parent function is:
`f(x)=√(x)`

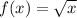
The transformed function is:
`g(x)=√(x-7) +7`

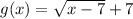
We need to find the statement that best describes the transformed function.

We know the transformation rule:

If f(x) is transformed into f(x)+c, then the function is transformed vertically c units up.

If f(x) is transformed into f(x)-c, then the function is transformed vertically c units down.

If f(x) is transformed into f(x-c) then the function is transformed right c units.

If f(x) is transformed into f(x+c) then the function is transformed left c units.

So, In the given transformation:

The parent function is:
`f(x)=x^2`

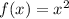
The transformed function is:
`g(x)=√(x-7) +7`

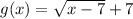
The transformed function is shifted 7 units up
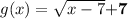`g(x)=√(x-7) \mathbf{ +7}` and 7 units right
`g(x)=\sqrt{x\mathbf{-7}} +7`

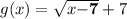
So, The correct option is:

The graph of g(x) is the graph of f(x) translated 7 units up and 7 units right.

Option A is correct option.