Question

A metallic sheet has a large number of slits, 5.0 mm wide and 20 cm apart, and is used as a diffraction grating for microwaves. A wide parallel beam of microwaves is incident normally on the sheet. What is the smallest microwave frequency for which only the central maximum occurs?

Answer 1

To solve this problem it is necessary to apply the concepts related to the principle of superposition and constructive interference, that is to say everything that refers to an overlap of two or more equal frequency waves, which when interfering create a new pattern of waves of greater intensity (amplitude) whose cusp is the antinode.

Mathematically its definition can be given as:

`d sin\theta =m\lambda`

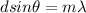
Where

d = Width of the slit

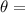`\theta =` Angle between the beam and the source

m = Order (any integer) which represent the number of repetition of the spectrum, at this case 1 (maximum respect the wavelength)

Since the point of the theta angle for which the diffraction becomes maximum will be when it is worth one then we have to:

`\lambda = d`

`\lambda = 20cm = 20*10^(-2)m`

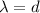
Applying the given relation of frequency, speed and wavelength then we will have that the frequency would be:

`f = (v)/(\lambda)`

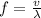
Here the velocity is equal to the speed of light and the wavelength to the value previously found.

`f = (3*10^8)/(0.2)`

`f = 1.5Ghz`

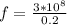
Therefore the smallest microwave frequency for which only the central maximum occurs is 1.5Ghz