Question

g A sample of 10 observations collected in a regression study on three variables, x_1(independent variable), x_2(independent variable and y(dependent variable). The sample resulted in the following data. SSR=26, SST=47 Using a 0.01 level of significance, we conclude that the regression model is significant overall. (Enter 1 if the conclusion is correct. Enter 0 if the conclusion is wrong.)

Answer 1

`p_v = P(F_(2,7) >4.3333)=0.0596`

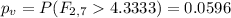
Since our p value it's higher than the significance level provided we can conclude that at 1% of significance we FAIL to reject the null hypothesis that the slopes for the inpendent variables are equal. So we don't have a significant effect on this case.

Explanation:

Analysis of variance (ANOVA) "is used to analyze the differences among group means in a sample".

The sum of squares "is the sum of the square of variation, where variation is defined as the spread between each individual value and the grand mean"

When we conduct a multiple regression we want to know about the relationship between several independent or predictor variables and a dependent or criterion variable.

If we assume that we have
`k` independent variables and we have
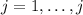`j=1,\dots,j` individuals, we can define the following formulas of variation:

`SS_(total)=\sum_(j=1)^n (y_j-\bar y)^2`

`SS_(regression)=SS_(model)=\sum_(j=1)^n (\hat y_(j)-\bar y)^2`

`SS_(error)=\sum_(j=1)^n (y_(j)-\hat y_j)^2`

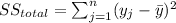
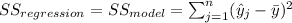
And we have this property

`SST=SS_(regression)+SS_(error)`

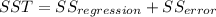
The degrees of freedom for the model on this case is given by
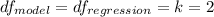`df_(model)=df_(regression)=k=2` where k =2 represent the number of independent variables.

The degrees of freedom for the error on this case is given by
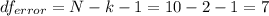`df_(error)=N-k-1=10-2-1=7`. Since for this case N=10 and k=2

And the total degrees of freedom would be
`df=N-1=10 -1 =9`

`SSE=SST-SSR=47-26=21`

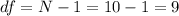
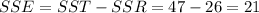
Now we can find the mean squares for the regression and the error, given by:

`MSR=(SSR)/(df_(regression))=(26)/(2)=13`

`MSE=(SSE)/(df_(error))=(21)/(7)=3`

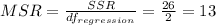
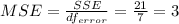
And now we can find the F statistic given by:

`F=(SSR)/(SSE)=(13)/(3)=4.333`

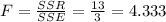
Now we can find the p value given by:

`p_v = P(F_(2,7) >4.333)=0.0596`

We can use the following excel code to verify the operation:"=1-F.DIST(4.3333,2,7,TRUE)"

Since our p value it's higher than the significance level provided we can conclude that at 1% of significance we FAIL to reject the null hypothesis that the slopes for the independent variables are equal. So we don't have a significant effect on this case.