Question

A cube has a density of 2000 kg/m3 while at rest in the laboratory. What is the cube's density as measured by an experimenter in the laboratory as the cube moves through the laboratory at 91.0 % of the speed of light in a direction perpendicular to one of its faces? You may want to review

Answer 1

kg/m³

Step-by-step explanation:

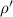`\rho'` = Actual density of cube = 2000 kg/m³

`\rho` = Density change due to motion

v = Velocity of cube = 0.91c

c = Speed of light =
`3* 10^8\ m/s`

Relativistic density is given by

`\rho=\frac{\rho'}{\sqrt{1-(v^2)/(c^2)}}\\\Rightarrow \rho=\frac{2000}{\sqrt{1-(0.91^2c^2)/(c^2)}}\\\Rightarrow \rho=(2000)/(√(1-0.91^2))\\\Rightarrow \rho=4823.8307\ kg/m^3`

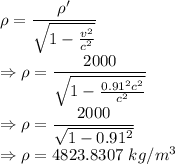
The cube's density as measured by an experimenter in the laboratory is 4823.8307 kg/m³