Question

A random sample of 146 recent donations at a certain blood bank reveals that 84 were type A blood. Does this suggest that the actual percentage of type A donations differs from 40%, the percentage of the population having type A blood? Carry out a test of the appropriate hypotheses using a significance level of 0.01. State the appropriate null and alternative hypotheses. H0: p = 0.40 Ha: p < 0.40 H0: p ≠ 0.40 Ha: p = 0.40 H0: p = 0.40 Ha: p ≠ 0.40 H0: p = 0.40 Ha: p > 0.40 Calculate the test statistic and determine the P-value. (Round your test statistic to two decimal places and your P-value to four decimal places.) z = P-value = State the conclusion in the problem context. Do not reject the null hypothesis.

1. There is not sufficient evidence to conclude that the percentage of type A donations differs from 40%. Do not reject the null hypothesis.
2. There is sufficient evidence to conclude that the percentage of type A donations differs from 40%. Reject the null hypothesis.
3. There is sufficient evidence to conclude that the percentage of type A donations differs from 40%. Reject the null hypothesis.
4. There is not sufficient evidence to conclude that the percentage of type A donations differs from 40%.

Would your conclusion have been different if a significance level of 0.05 had been used?
a. Yes
b. No

Answer 1

There is sufficient evidence to conclude that the percentage of type A donations differs from 40%. Reject the null hypothesis.

Conclusion wouldn't be different if a significance level of 0.05 had been used.

Explanation:

null and alternative hypotheses are

H0: p = 0.40

Ha: p ≠ 0.40

test statistic can be calculated as:

z=
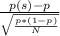`\frac{p(s)-p}{\sqrt{(p*(1-p))/(N) } }` where

• p(s) is the sample proportion of having type A blood (
  `(84)/(146) =0.575`

• p is the proportion assumed under null hypothesis. (0.40)

• N is the sample size (146)

then z=
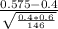`\frac{0.575-0.4}{\sqrt{(0.4*0.6)/(146) } }` ≈4.32

the p-value is ≈0.00002 <0.01

Conclusion:

There is sufficient evidence to conclude that the percentage of type A donations differs from 40%. Reject the null hypothesis.

Conclusion wouldn't be different if a significance level of 0.05 had been used since 0.00002 <0.05