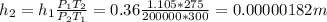Answer:
a. 0.000002 m
b. 0.00000182 m
Step-by-step explanation:
36 cm = 0.36 m
15 cm = 0.15 m
a) We can start by calculating the air-water pressure of the bucket submerged 20m below the water surface:
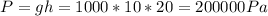
Suppose air is ideal gas, then if the temperature stays the same, the product of its pressure and volume stays the same
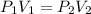
Where P1 = 1.105 Pa is the atmospheric pressure, V_1 is the air volume in the bucket on the suface:

As the pressure increases, the air inside the bucket shrinks. But the crossection area stays constant, so only h, the height of air, decreases:
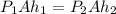
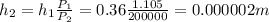
b) If the temperatures changes, we can still reuse the ideal gas equation above: