Question

Need some help, it’s a little confusing to understand..

Answer 1

`-1.75`

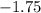
Explanation:

It can help to write some or all of the terms of the series. This can help you identify the first term as -7/3 and the common ratio as -1/3. Then the formula for the sum of a geometric series can be used to find the sum of 6 terms.

`=7\left((-1)/(3)\right)^1+7\left((-1)/(3)\right)^2+7\left((-1)/(3)\right)^3+7\left((-1)/(3)\right)^4+7\left((-1)/(3)\right)^5+7\left((-1)/(3)\right)^6\\\\S_6=a_1\cdot(r^6-1)/(r-1) \quad\text{for $a_1=-7/3$ and r=-1/3}\\\\S_6=\left((-7)/(3)\right)\left((\left((-1)/(3)\right)^6-1)/((-1)/(3)-1)\right)=\left((-7)/(3)\right)\left(((-728)/(729))/((-4)/(3))\right)=((-7)(728)(3))/((3)(729)(4))`

`S_6=((-7)(182))/(729)=-(1274)/(729)\approx -1.75`

___

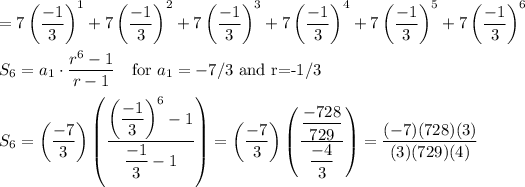
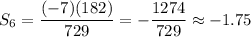
Or, you can simply add up the terms on your calculator.

-2.33333 +0.777778 -0.259259 +0.0864198 -0.0288066 +0.00960219

The first two or three terms will get you a sum close enough to choose the correct answer.