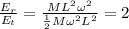Question

A dumbbell consists of two point-like masses M connected by a massless rod of length 2L. There are no external forces. If the dumbbell rotates with angular velocity w while its center of mass moves linearly (translates) with velocity v such that v = ωL, the ratio of the rotational kinetic energy to the translational (linear) kinetic energy is:

Answer 1

2

Step-by-step explanation:

The rotational kinetic energy of the dumbbell is:

`E_r = (1)/(2)I\omega^2`

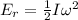
where I is the moments of inertia of the two point-like system

`I = 2Mr^2 = 2ML^2`

`E_r = ML^2\omega^2`

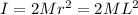
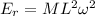
The translation kinetic energy is:

`E_t = (1)/(2)Mv^2 = (1)/(2)M\omega^2L^2`

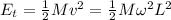
Therefore the ratio of the rotational kinetic energy to the translational (linear) kinetic energy is:

`(E_r)/(E_t) = (ML^2\omega^2)/((1)/(2)M\omega^2L^2) = 2`