Answer:
The one that makes more sense for our conclusion is that the rocket crashes approximately 6.299601 seconds after it has been launched given the path of the rocket is
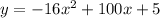 .
.
Explanation:
The rocket has crashed on the ground when the height between the ground and the rocket is 0.
We want to find the time,
 , such that the height,
, such that the height,
 , is 0.
, is 0.
We are going to solve the following equation:
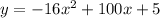 with
with

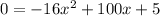
Upon comparing this equation to
 , I see that I have the following values for
, I see that I have the following values for
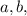 and
and
 :
:

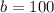
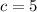
The quadratic formula is:
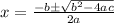 .
.
Let's plug in the values we got above now.
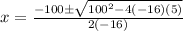
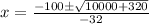

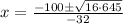

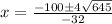
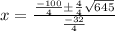
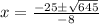
This gives us either:
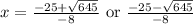
Let's punch both of these into the calculator:
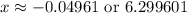
The one that makes more sense for our conclusion is that the rocket crashes approximately 6.299601 seconds after it has been launched.