Answer:
a) y = 162.6 m , b) R = 928.64 m
Step-by-step explanation:
We will solve this exercise using projectile launch kinematics, as the initial velocities and angle are equal on the planet and the Earth, let's look for the gravedd coinage of the planet
Earth
R = v₀² sin 2θ / g
R g = v₀² sin 2θ
In the planet
4.8 R = v₀² sin 2θ /

4.8 R
 = v₀² sin 2θ
= v₀² sin 2θ
4.8 R
 = R g
= R g
 = g / 4.8
= g / 4.8
 = 9.8 / 4.8
= 9.8 / 4.8
 = 2.04 m / s²
= 2.04 m / s²
Now we can answer the questions
a) The maximum height
Vy² =
 ² - 2 g y
² - 2 g y
For ymax the vertical speed is zero (
 = 0)
= 0)
sin θ =
 /
/
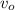
 =
=
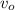 sinθ
sinθ
 = 44.9 sin 35
= 44.9 sin 35
 = 25.75 m/s
= 25.75 m/s
y =
 ²/2
²/2

y = 25.75² / (2 2.04)
y = 162.6 m
b) the scope
R = v₀² sin 2θ /

R = 44.9² sin 2 35 / 2.04
R = 928.64 m