Question

The number of nuts in a can of mixed nuts is found to be normally distributed, with a mean of 500 nuts and a standard deviation of 20 nuts. My can of mixed nuts has only 443 nuts. What is the z-score for this can of nuts? (Enter your answer to two decimal places.)

Answer 1

Answer: the z score is - 2.85

Explanation:

The number of nuts in a can of mixed nuts is found to be normally distributed. The formula for normal distribution is expressed as

z = (x - u)/s

Where

x = number of nuts

u = mean number of nuts

s = standard deviation

From the information given,

u = 500 nuts

s = 20 nuts

x = 443

To determine z,

z = ( 443 - 500)/20 = - 2.85

Answer 2

z = -2.85

Explanation:

Since the number of nuts per can is normally distributed:

Mean number of nuts (μ)= 500 nuts

Standard Deviation (σ)= 20 nuts

X = 443 nuts

For any given number of nuts X, the z-score is given by:

`z=(X-\mu)/(\sigma) =(443-500)/(20)\\z= -2.85`

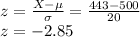
The z-score for this can of nuts with 443 nuts is -2.85.