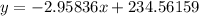Question

Some types of algae have the potential to cause damage to river ecosystems. Suppose the accompanying data on algae colony density (y) and rock surface area (x) for nine rivers is a subset of data that appeared in a scatterplot in a research paper in a scientific journal. Col1 x 50 55 50 79 44 37 70 45 49 Col2 y 152 48 22 35 43 171 13 185 25 (a) Compute the equation of the least-squares regression line. (Round your numerical values to five decimal places.)

Answer 1

`y=-2.95836 x +234.56159`

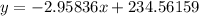
Explanation:

We assume that th data is this one:

x: 50, 55, 50, 79, 44, 37, 70, 45, 49

y: 152, 48, 22, 35, 43, 171, 13, 185, 25

a) Compute the equation of the least-squares regression line. (Round your numerical values to five decimal places.)For this case we need to calculate the slope with the following formula:

`m=(S_(xy))/(S_(xx))`

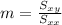
Where:

`S_(xy)=\sum_(i=1)^n x_i y_i -((\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i))/(n)`

`S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)`

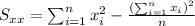
So we can find the sums like this:

`\sum_(i=1)^n x_i =50+ 55+ 50+ 79+ 44+ 37+ 70+ 45+ 49=479`

`\sum_(i=1)^n y_i =152+ 48+ 22+ 35+ 43+ 171+ 13+ 185+ 25=694`

`\sum_(i=1)^n x^2_i =50^2 + 55^2 + 50^2 + 79^2 + 44^2 + 37^2 + 70^2 + 45^2 + 49^2=26897`

`\sum_(i=1)^n y^2_i =152^2 + 48^2 + 22^2 + 35^2 + 43^2 + 171^2 + 13^2 + 185^2 + 25^2=93226`

`\sum_(i=1)^n x_i y_i =50*152+ 55*48+ 50*22+ 79*35+ 44*43+ 37*171+ 70*13+ 45*185+ 49*25=32784`

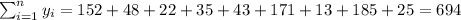
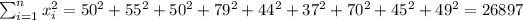
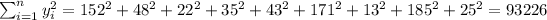
With these we can find the sums:

`S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)=26897-(479^2)/(9)=1403.556`

`S_(xy)=\sum_(i=1)^n x_i y_i -\frac{(\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i)}=32784-(479*694)/(9)=-4152.22`

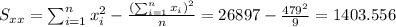
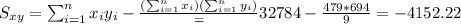
And the slope would be:

`m=-(-4152.222)/(1403.556)=-2.95836`

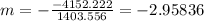
Nowe we can find the means for x and y like this:

`\bar x= (\sum x_i)/(n)=(479)/(9)=53.222`

`\bar y= (\sum y_i)/(n)=(694)/(9)=77.111`

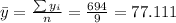
And we can find the intercept using this:

`b=\bar y -m \bar x=77.1111111-(-2.95836*53.22222222)=234.56159`

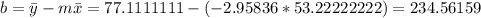
So the line would be given by:

`y=-2.95836 x +234.56159`