Question

A shoe manufacturer compared material A and material B for the soles of shoes. Twelve volunteers each got two shoes. The left was made with material A and the right with material B. On both shoes, the material was 1 inch thick. Volunteers used the shoes normally for two months and returned them to the manufacturer. Technicians then measured the thickness of the soles and recorded the amount of wear (in microns):

Volunteer 1 2 3 4 5 6 7 8 9 10 11 12
Sole A 379 378 328 372 325 304 356 309 354 318 355 392
Sole B 372 376 328 368 283 252 369 321 379 303 328 411

They wish to test
H0: µA −µB = 0
against
HA: µA −µB 6= 0,

where µA and µB are the unknown population mean amounts of sole wear, using α = 0.05.

(a) Are the two samples paired or independent? Explain your answer.
(b) Make a normal QQ plot of the differences within each pair. Is it reasonable to assume a normal population of differences?
(c) Choose a test appropriate for the hypotheses above and justify your choice based on your answers to parts (a) and (b). Perform the test by computing a p-value, make a test decision, and state your conclusion in the context of the problem

Answer 1

a) Are dependent since we are mesuring at the same individuals but on different times and with a different method

b) If we see the qq plot we don't have any significant deviation for the values and we don't have any heavy tail so we can conclude that we can approximate the differences with the normal distribution.

c)
`p_v =P(t_((12))>0.969) =0.353`

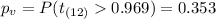
So the p value is higher than the significance level given, so then we can conclude that we FAIL to reject the null hypothesis. So we can conclude that the mean differences is NOT significantly different from 0 .

Explanation:

A paired t-test is used to compare two population means where you have two samples in which observations in one sample can be paired with observations in the other sample. For example if we have Before-and-after observations (This problem) we can use it.

The Q-Q plot, or quantile-quantile plot, "is a graphical tool to help us assess if a set of data plausibly came from some theoretical distribution such as a Normal or exponential".

Let put some notation

x=value for A , y = value for B

A: 379, 378, 328, 372, 325, 304, 356, 309, 354, 318, 355, 392

B: 372, 376, 328, 368, 283, 252, 369, 321, 379, 303, 328, 411

(a) Are the two samples paired or independent? Explain your answer.

Are dependent since we are mesuring at the same individuals but on different times and with a different method

(b) Make a normal QQ plot of the differences within each pair. Is it reasonable to assume a normal population of differences?

The first step is calculate the difference
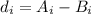`d_i=A_i-B_i` and we obtain this:

d: 7,2,0,4,42,52,-13,-12,-25,15,27,-19

In order to do the qqplot we can use the following R code:

d<-c(7,2,0,4,42,52,-13,-12,-25,15,27,-19)

qqnorm(d)

And the graph obtained is attached.

If we see the qq plot we don't have any significant deviation for the values and we don't have any heavy tail so we can conclude that we can approximate the differences with the normal distribution.

(c) Choose a test appropriate for the hypotheses above and justify your choice based on your answers to parts (a) and (b). Perform the test by computing a p-value, make a test decision, and state your conclusion in the context of the problem

The system of hypothesis for this case are:

Null hypothesis:
`\mu_A- \mu_B = 0`

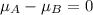
Alternative hypothesis:
`\mu_A -\mu_B \\eq 0`

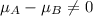
The second step is calculate the mean difference

`\bar d= (\sum_(i=1)^n d_i)/(n)= (80)/(12)=6.67`

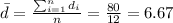
The third step would be calculate the standard deviation for the differences, and we got:

`s_d =(\sum_(i=1)^n (d_i -\bar d)^2)/(n-1) =23.849`

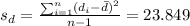
The 4 step is calculate the statistic given by :

`t=(\bar d -0)/((s_d)/(√(n)))=(6.67 -0)/((23.849)/(√(12)))=0.969`

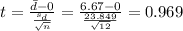
The next step is calculate the degrees of freedom given by:

`df=n-1=12-1=11`

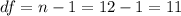
Now we can calculate the p value, since we have a two tailed test the p value is given by:

`p_v =P(t_((12))>0.969) =0.353`

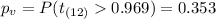
So the p value is higher than the significance level given, so then we can conclude that we FAIL to reject the null hypothesis. So we can conclude that the mean differences is NOT significantly different from 0 .