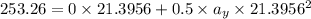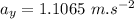Question

Two cars start from rest at a red stop light. When the light turns green, both cars accelerate forward. The blue car accelerates uniformly at a rate of 4.3 m/s2 for 3.3 seconds. It then continues at a constant speed for 14.3 seconds, before applying the brakes such that the car’s speed decreases uniformly coming to rest 253.26 meters from where it started. The yellow car accelerates uniformly for the entire distance, finally catching the blue car just as the blue car comes to a stop.

1)

How fast is the blue car going 2.6 seconds after it starts?

How fast is the blue car going 7.2 seconds after it starts?

How far does the blue car travel before its brakes are applied to slow down?

What is the acceleration of the blue car once the brakes are applied?

What is the total time the blue car is moving?

What is the acceleration of the yellow car?

Answer 1

`v_(2.6b)=11.18\ m.s^(-1)`

`v_(7.2b)=14.19\ m.s^(-1)`

`s_(bb)=226.3305\ m`

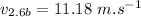
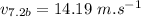
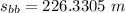
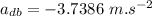`a_(db)=-3.7386\ m.s^(-2)` negative sign denotes deceleration.

`t_b=21.3956\ s`

`a_y=1.1065\ m.s^(-2)`

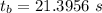
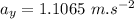
Step-by-step explanation:

Given:

• initial speed of blue car,
  `u_b=0\ m.s^(-1)`

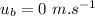
• initial speed of yellow car,
  `u_y=0\ m.s^(-1)`

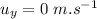
• acceleration rate of blue car,
  `a_b=4.3\ m.s^(-2)`

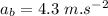
• time for which the blue car accelerates,
  `t_(ab)=3.3\ s`

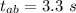
• time for which the blue car moves with uniform speed before decelerating,
  `t_(ub)=14.3\ s`

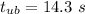
• total distance covered by the blue car before coming to rest,
  `s_b=253.26 \ m`

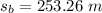
• distance at which the the yellow car intercepts the blue car just as the blue car come to rest,
  `s_y=253.26 \ m`

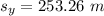
1)

Speed of blue car after 2.6 seconds of starting the motion:

Applying the equation of motion:

`v_(2.6b)=u_b+a_b.t`

`v_(2.6b)=0+4.3* 2.6`

`v_(2.6b)=11.18\ m.s^(-1)`

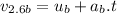
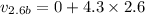
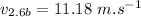
Speed of blue car after 7.2 seconds of starting the motion:

∵The car accelerates uniformly for 3.3 seconds after which its speed becomes uniform for the next 14.3 second before it applies the brake.

so,

`v_(7.2b)=u+a_b* t_(ab)`

`v_(7.2b)=0+4.3* 3.3`

`v_(7.2b)=14.19\ m.s^(-1)`

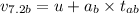
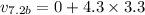
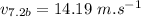
Distance travelled by the blue car before application of brakes:

This distance will be
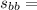`s_(bb)=` (distance travelled during the accelerated motion) + (distance travelled at uniform motion)

Now the distance travelled during the accelerated motion:

`s_(ab)=u_b.t_(ab)+(1)/(2) a_(b).t_(ab)^2`

`s_(ab)=0* 3.3+0.5* 4.3* 3.3^2`

`s_(ab)=23.4135\ m`

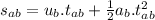
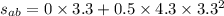
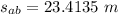
Now the distance travelled at uniform motion:

`s_(ub)=14.19* 14.3`

`s_(ub)=202.917\ m`

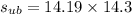
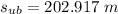
Finally:

`s_(bb)=s_(ab)+s_(ub)`

`s_(bb)=23.4135+202.917`

`s_(bb)=226.3305\ m`

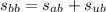
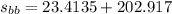
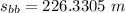
Acceleration of the blue car once the brakes are applied

Here we have:

initial velocity,
`u=14.19\ m.s^(-1)`

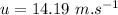
final velocity,
`v=0\ m.s^(-1)`

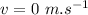
distance covered while deceleration,
`s_(db)=s_b-s_(bb)`

`\Rightarrow s_(db)=253.26 -226.3305=26.9295\ m`

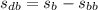
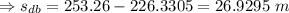
Using the equation of motion:

`v^2=u^2+2a_(db).s_(db)`

`0^2=14.19^2+2* a_(db)* 26.9295`

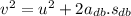
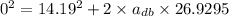
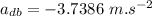`a_(db)=-3.7386\ m.s^(-2)` negative sign denotes deceleration.

The total time for which the blue car moves:

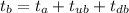`t_b=t_a+t_(ub)+t_(db)` ........................(1)

Now the time taken to stop the blue car after application of brakes:

Using the eq. of motion:

`v=u+a_(db).t_(db)`

`0=14.19-3.7386* t_(db)`

`t_(db)=3.7956\ s`

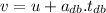
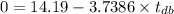
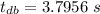
Putting respective values in eq. (1)

`t_b=3.3+14.3+3.7956`

`t_b=21.3956\ s`

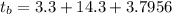
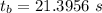
For the acceleration of the yellow car:

We apply the law of motion:

`s_y=u_y.t_y+(1)/(2) a_y.t_y^2`

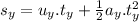
Here the time taken by the yellow car is same for the same distance as it intercepts just before the stopping of blue car.

Now,

`253.26=0* 21.3956+0.5* a_y* 21.3956^2`

`a_y=1.1065\ m.s^(-2)`