Question

Vertically polarized light with an intensity of 235 W/m 2passes through a polarizer with a vertical axis. Then it goes through a second polarizer, and emerges with an intensity of 69.3 W/m 2 . What is the angle of the second polarizer with respect to the first one?

Answer 1

To solve this problem we must use the concepts related to the Law of Malus and the intensity of light. The intensity of a linearly polarized beam of light, which passes through a perfect analyzer and vertical optical axis is equivalent to:

`I= I_0cos^2 \theta`

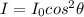
Where,

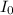`I_(0)` indicates the intensity of the light before passing through the polarizer

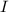`I` is the resulting intensity

`\theta` indicates the angle between the axis of the analyzer and the polarization axis of the incident light.

Since the light has the same intensity after the first polarizer we approach the second intensity directly so

`I_2 = I_0cos^2 \theta`

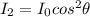
Our values are given as :

`I_2 = 69.3W/m^2`

`I_0 = 235W/m^2`

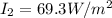
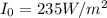
Therefore replacing and re-arrange to find the angle we have

`69.3 =  235cos^2 \theta`

`0.2948 = cos^2\theta`

`\theta = cos^(-1)( √(0.2948))`

`\theta = 57.1\°`

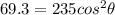
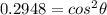
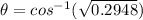
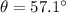
Therefore the angle of the second polarizer with respect to the first one is 57.1°