Question

In poker, there is a 52 card deck with 4 cards each of each of 13 face values. A full house is a hand of 5 cards with 3 of one face value, and 2 of another. What is the probability that a random poker hand is a full house? You can leave your answer in terms of bionomial co-efficients and similar factors, but please explain each term.

Answer 1

`P(FH) = \frac{\binom{13}{1}*\binom{4}{3}*\binom{12}{1}*\binom{4}{2}}{\binom{52}{5}}`

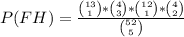
P(FH) =0.00144

Explanation:

The total number of possible poker hands (n) is the combination of 5 out of 52 cards:

`n=\binom{52}{5}`

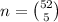
In order to get a full house, first pick one out of 13 cards (13 choose 1), then pick 3 out of the 4 cards of the chosen type to form three of a kind (4 choose 3), now pick another card from the remaining 12 different numbers or faces (12 choose 1), then pick 2 out of the 4 suits to form a pair (4 choose 2)

The probability of getting a fullhouse, in binomial coefficients is:

`P(FH) = \frac{\binom{13}{1}*\binom{4}{3}*\binom{12}{1}*\binom{4}{2}}{\binom{52}{5}}`

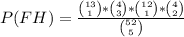
Expanding the coefficients and solving:

`P(FH) = (13*4*12*(4*3)/(2*1) )/((52*51*50*49*48)/(5*4*3*2))\\P(FH) =0.00144`