Question

Tickets were sold to the public for 8.00$ each and sold to students for 3.00$ a piece. There were a total of 400 tickets sold. Making a total revenue of 1900.00$. How many tickets were sold to the public and how many tickets were sold to students

Answer 1

140 tickets were sold to public and 260 tickets were sold to students

Solution:

Let "p" be the number of tickets sold to public

Let "s" be the number of tickets sold to students

Cost of one ticket sold to public = $ 8.00

Cost of one ticket sold to student = $ 3.00

There were a total of 400 tickets sold

number of tickets sold to public + number of tickets sold to students = 400

p + s = 400 -------- eqn 1

Making a total revenue of 1900.00$

number of tickets sold to public x Cost of one ticket sold to public + number of tickets sold to students x Cost of one ticket sold to student = 1900.00

`p * 8.00 + s * 3.00 = 1900.00`

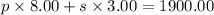
8p + 3s = 1900 ------ eqn 2

Let us solve eqn 1 and eqn 2 to find values of "p" and "s"

Multiply eqn 1 by 3

3p + 3s = 1200 ---- eqn 3

Subtract eqn 3 from eqn 2

8p + 3s = 1900

3p + 3s = 1200

(-) ------------------

5p = 700

p = 140

Substitute p = 140 in eqn 1

p + s = 400

140 + s = 400

s = 260

Thus 140 tickets were sold to public and 260 tickets were sold to students