Question

A typical home may require a total of 2.00*10^3kWh of energy per month. Suppose you would like to obtain this energy from sunlight, which has an average daylight intensity of 1400 W/m^2 . Assuming that sunlight is available 8.0h per day, 25 d per month (accounting for cloudy days), and that you have a way to store energy from your collector when the Sun isn't shining, determine the smallest collector size that will provide the needed energy, given a conversion efficiency of 24% .

Answer 1

Smallest collector size≈30
`m^(2)`

Step-by-step explanation:

Daily sunlight intensity = 1400
`w/m^(2)`.

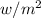For a collector of 24% efficiency, the absorption per day per
`m^(2)`

= 0.24*1400 = 336
`w/m^(2)`.

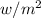For 8 hours, 25days of available sunlight, energy absorbed by collector per metre square , will be = 8* 25 *336 = 67200wh.

This is the amount of sunlight energy which will be trapped by 1
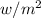`w/m^(2)`. of collector in a month.

To find how many metre square of collector is required to get 2*
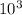`10^(3)`kwh, we simply divide the required energy by the amount absorbed per square metre.

Smallest size of collected needed =
`(2.00*1000*10^(3))/(67200)`

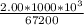
=29.76

≈30
`m^(2)`