Question

A person exerts a tangential force of 37.7 N on the rim of a disk-shaped merry-go-round of radius 2.75 m and mass 144 kg. If the merry-go-round starts at rest, what is its angular speed after the person has rotated it through an angle of 33.2°?

Answer 1

ω = 0.467 rad/s

Step-by-step explanation:

given,

tangential force exerted by the person = 37.7 N

radius of merry-go-round = 2.75 m

mass of merry-go-round = 144 Kg

angle = 33.2°

moment of inertia

`I = (1)/(2) m R^2`

`I = (1)/(2)* 144 * 2.75^2`

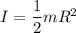
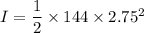
I = 544.5 kg.m²

torque = force x radius

τ = 37.7 x 2.75

τ = 103.675 N.m

angular acceleration

`\alpha= (\tau)/(I)`

`\alpha= (103.675)/(544.5)`

α = 0.190 rad/s²

now ,

distance =
`33.2* \dfrca{2\pi}{360}`

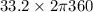
d = 0.579 rad

we know,

using equation of rotational motion

`d = \omega t + (1)/(2)\alpha t^2`

`0.579 = (1)/(2)* 0.190* t^2`

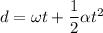
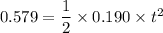
t = 2.46 s

angular speed

ω = α x t

ω = 0.19 x 2.46

ω = 0.467 rad/s