Question

A solid wood door 1.00 m wide and 2.00 m high is hinged along one side and has a total mass of 43.0 kg. Initially open and at rest, the door is struck at its center by a handful of sticky mud with mass 0.600 kg kg, traveling perpendicular to the door at 11.0 m/s just before impact.

Answer 1

w_f = 0.2270 rad/sec

Step-by-step explanation:

I am assuming that we have to find the angular speed of door.

This question involves the concept of conservation of angular momentum. It is an inelastic or "sticky" collision. So, momentum is conserved and kinetic energy is lost. The final angular momentum will include both masses since the mud sticks to the door.

L=angular momentum = Ixω (moment of inertia times angular velocity) = r x p = r x m× v (radius times momentum which is mass times velocity)

Therefore,

L(initial)=L(final)

I of the door: The moment of inertia for a thin rectangular plate rotating about an axis on its edge is (1/3)ma^2 where a is the distance from the axis or in this case the width of the door.

L(mud)= r x m x v = (0.5) x (0.6) x (11) = 3.30
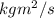`kgm^2/s`= L(initial)

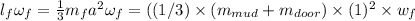`l_f\omega_f=(1)/(3)m_fa^2\omega_f=((1/3)*(m_(mud) + m_(door))* (1)^2* w_f` = 3.30

`3.30=((1/3)*(43.6)*1)* w_f`

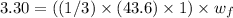
solving the above we get

w_f = 0.2270 rad/sec