Answer:
a) I = 0.42358 Kg*m^2
b) K = 1203.99 J
Step-by-step explanation:
a) The moment of inertia is:
I =
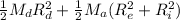
where
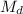 is the mass of the disk,
is the mass of the disk,
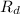 is the radius of the disk,
is the radius of the disk,
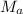 the mass of the annular cylinder,
the mass of the annular cylinder,
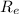 is the outer radius of the cylinder and
is the outer radius of the cylinder and
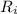 the inner radius of the cylinder.
the inner radius of the cylinder.
Replacing values, we get:
I =
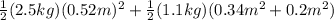
I = 0.42358 Kg*m^2
b) First, we will change the angular velocity from rev/s to rad/s as:
W = 12*2
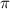 rad/s
rad/s
W = 75.398 rad/s
Also the kinetic energy K is:
K =
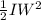
Where I is the moment of inertia and W is the angular velocity in rad/s.
so, replacing values, we get:
K =
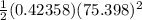
K = 1203.99 J