To solve this problem it is necessary to apply the related concepts to string vibration. This concept shows the fundamental frequency of a string due to speed and length, that is,
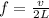
Where
v = Velocity
L = Length
Directly if the speed is maintained the frequency is inversely proportional to the Length:

Therefore the relationship between two frequencies can be described as
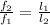
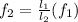
Our values are given as,
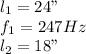
Therefore the second frequency is
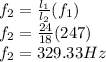
The frequency allocation of 329Hz is note E.