Question

six people, including A,B, and C, form a queue in a random order (all 6! orderings are equiprobable). Consider the event "B is between A and C in the queue". What is its probability? (The order of A and C can be arbitrary, but B should be between them)

Answer 1

1/15

Explanation:

ways 6 people can form a que= 6!= 720

ways A,B and C form a que such that B is in the middle= 2

A,B,C and C,B,A

Now if the arrangement is A,B,C then ABC and rest of the three people can arrange themselves in 4! ways

Likewise, if the arrangement is C,B,A then ABC and rest of the three people can arrange themselves in 4! ways

So the total number of ways in which six people can arrange themselves with B always in between A and C is

4! × 2= 48

Probability of event B is between A and C in the queue= 48/720 = 1/15

Answer 2

There is a 1.39% probability that "B is between A and C in the queue".

Explanation:

The first step to solve this problem is find the total number of possible orderings:

The first person of the queue can be any of the six. The second, can be any but the first, so five.

So

There are 6*5*4*3*2*1 = 720 total queue orderings.

Now we find the number of queues that B is between A and C. So:

We have:

B as the second, A as the first and C as the third

B as the second, C as the first and A as the third

B as the third, A as the second and C as the fourth

B as the third, C as the second and A as the fourth

B as the fourth, A as the third and C as the fifth.

B as the fourth, C as the third and A as the fifth.

B as the fifth, A as the fourth and C as the sixth.

B as the fifth, C as the fourth and A as the sixth.

So 8 total outcomes in which B is between A and C.

What is its probability?

`P = (8)/(720) = 0.0111`

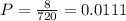
There is a 1.11% probability that "B is between A and C in the queue".