Question

Starting at home, Ishaan traveled uphill to the grocery store for 12 minutes at just 15 mph. He then traveled back home along the same path downhill at a speed of 30 mph

Answer 1

Question is Incomplete, Complete Question is given below.

Starting at home, Ishaan traveled uphill to the grocery store for 12 minutes at just 15 mph. He then traveled back home along the same path downhill at a speed of 30 mph. What is his average speed for the entire trip from home to the grocery store and back?

Answer:

The average speed for the entire trip from home to the grocery store and back is 20 mph.

Explanation:

Given:

Ishaan traveled uphill to the grocery store for 12 minutes at just 15 mph.

Time taken by him = 12 minutes

Speed = 15 mph

Since since speed is given in miles per hour and time is in minute, So we convert time in hour.

Time taken by him =
`(12)/(60) =(1)/(5) \ hrs`

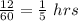
Now Distance can be calculate by Multiplying speed with time.

So, distance traveled = Speed × time

Substituting the values we get;

Distance traveled =
`15 * (1)/(5) =3 \ miles`

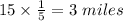
Now Again, he traveled back home along the same path downhill = 3 miles

Speed of covering downhill = 30 mph

We will find the time required with this speed to travel the distance.

Time Taken =
`(Distance)/(Speed) = (3)/(30) =(1)/(10) \ hrs`

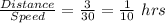
Now We need to find the Average speed.

Average speed can be calculated by dividing Total Distance with Total Time.

Average Speed =
`(Total \ Distance)/(Total \ Time)`

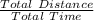
Average Speed =
`(3+3)/((1)/(5)+(1)/(10))`

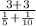
Making denominators common by taking LCM we get;

Average Speed =
`(3+3)/((1* 2)/(5* 2)+(1*1)/(10* 1)) = (6)/((2)/(10)+(1)/(10))= (6)/((2+1)/(10))= (6*10)/(3) = (60)/(3) =20 \ mph`

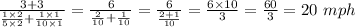
Hence Average speed for the entire trip from home to the grocery store and back is 20 mph.