Question

During a concert, $3280 was received. A total of 760 people attended. Reserved seats were $6 and general admission seats were $4. How many of each kind of ticket was sold?

Answer 1

The number of reserved seat is 120 and number of general seat is 640.

Explanation:

Given,

Total number of seats = 760

Total collected Money = $3280

Solution,

Let the total number of reserved seat be x.

And the total number of general seat be y

Hence total number of seats is the sum of total number of reserved seat and the total number of general seats.

So the equation can be written as;

`x+y=760\ \ \ \ equation\ 1`

Again, total money collected is the sum of fees of one reserved seat times total number of reserved seat and fees of one general seat times the total number of general seats.

So the equation can be written as;

`6x+4y=3280\ \ \ \ \ equation\ 2`

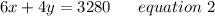
Now, multiplying equation 1 by 4 and then subtract it from equation 2.

`4x+4y=3040`

`(6x+4y)-(4x+4y)=3280-3040\\\\2x=240\\\\x=(240)/(2)=120`

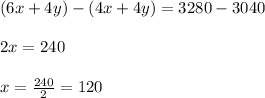
On substituting the value of x in equation 1, we get;

`x+y=760\\120+y=760\\y=760-120=640`

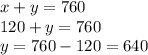
Thus the number of reserved seat is 120 and number of general seat is 640.