Answer: E= 0.107
Explanation:
Formula to find the margin of error :
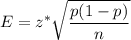
, where n= sample size .
p= sample proportion
z* = critical value.
Given : Sample size : n= 62
Number of red candies out of 62 = 15
Proportion of red candies =

We know that , the critical value for 95% confidence = z*= 1.96 [Using z-table]
Then,


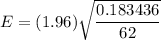
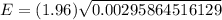

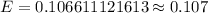
Hence, the margin of error = E= 0.107