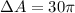Question

The total surface area for a silo (base with radius r, cylindrical side with height h, hemispherical cap) is A = 3πr2 + 2πrh. Suppose h and r are measured to be h = 20 feet and r = 8 feet to within an error of 1 2 foot for h and 1 4 foot for r. Use differentials to estimate the maximum possible error for A (in square feet).

Answer 1

`\Delta A=30\pi ft^2`

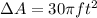
Explanation:

The total surface area for a silo A = 3πr^2 + 2πrh.

given

base radius r, cylindrical side with height h, hemispherical cap

h=20 ft r=8 ft

Δh= 1/2 ft and Δr= 1/4 ft

now, diffrentiating we get

dA= 3π×2r×dr+2π(r×dh+Δr×h)

putting values we get

`\Delta A= 6\pi\Delta r+2\pi r\Delta h+2\pi h \Delta r`

`\Delta A= (6\pi\ r+2\pi h)\Delta r+2\pi r \Delta h`

`\Delta A= (6\pi\ 8+2\pi 20)\(1/4)+2\pi 8(1/2)`

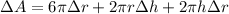
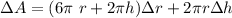
solving the above equation we get

`\Delta A=30\pi`