Question

10. A 20.00 mL sample of 0.150 mol/L ammonia (NH3(aq)) is titrated to the equivalence point by 20.0 mL of a solution of 0.150 mol/L of the strong acid hydroiodic acid (HI (aq)).

a) Write a balanced equation for the titration reaction.
b) What is the pH of the ammonia solution before the titration begins?
c) What is the pH at the equivalence point?

Answer 1

`\large \boxed{\rm a)\, NH_(3)(aq) + \text{HI}(aq) \, \longrightarrow \, \,$ NH_(4)^(+)(aq) +\text{I}^(-)(aq);\,b)\,11.22;\, c)\, 5.19}`

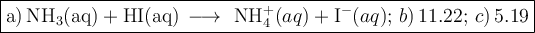
Step-by-step explanation:

a) Balanced equation

The balanced chemical equation for the titration is

`\large \boxed{\rm NH_(3)(aq) + \text{HI}(aq) \, \longrightarrow \, \,$ NH_(4)^(+)(aq) +\text{I}^(-)(aq)}`

b) pH at start

For simplicity, let's use B as the symbol for NH₃.

The equation for the equilibrium is

`\rm B + H_(2)O \, \rightleftharpoons\,BH^(+) + OH^(-)`

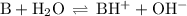
(i) Calculate [OH]⁻

We can use an ICE table to do the calculation.

B + H₂O ⇌ BH⁺ + OH⁻

I/mol·L⁻¹: 0.150 0 0

C/mol·L⁻¹: -x +x +x

E/mol·L⁻¹: 0.150 - x x x

`K_{\text{b}} = \frac{\text{[BH}^(+)]\text{[OH}^(-)]}{\text{[B]}} = 1.8 * 10^(-5)\\\\(x^(2))/(0.150 - x) = 1.8 * 10^(-5)`

Check for negligibility:

`(0.150 )/(1.8 * 10^(-5)) = 8300 > 400\\\\x \ll 0.150`

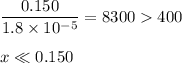
(ii) Solve for x

`(x^(2))/(0.150) = 1.8 * 10^(-5)\\\\x^(2) = 0.150 * 1.8 * 10^(-5)\\x^(2) = 2.7 * 10^(-6)\\x = \sqrt{2.7 * 10^(-6)}\\x = \text{[OH]}^(-) = 1.64 * 10^(-3) \text{ mol/L}`

(iii) Calculate the pH

`\text{pOH} = -\log \text{[OH}^(-)] = -\log(1.64 * 10^(-3)) = 2.78\\\\\text{pH} = 14.00 - \text{pOH} = 14.00 - 2.78 = \mathbf{11.22}\\\\\text{The pH of the solution at equilibrium is } \large \boxed{\mathbf{11.22}}`

(c) pH at equivalence point

(i) Calculate the moles of each species

`\text{Moles of B} = \text{Moles of HI} = \text{20.00 mL} * \frac{\text{0.0150 mmol}}{\text{1 mL}} = \text{3.00 mmol}`

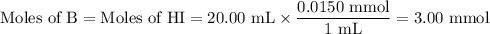
B + HI ⇌ BH⁺ + I⁻

I/mol: 3.00 3.00 0

C/mol: -3.00 -3.00 +3.00

E/mol/: 0 0 3.00

(ii) Calculate the concentration of BH⁺

At the equivalence point we have a solution containing 3.00 mmol of NH₄I

Volume = 20.00 mL + 20.00 mL = 40.00 mL

`\rm [BH^(+)] = \frac{\text{3.00 mmol}}{\text{40.00 mL}} = \text{0.0750 mol/L}`

(iii) Calculate the concentration of hydronium ion

We can use an ICE table to organize the calculations.

BH⁺+ H₂O ⇌ H₃O⁺ + B

I/mol·L⁻¹: 0.0750 0 0

C/mol·L⁻¹: -x +x +x

E/mol·L⁻¹: 0.0750 - x x x

`K_{\text{a}} = \frac{K_{\text{w}}} {K_{\text{b}}} = (1.00 * 10^(-14))/(1.8 * 10^(-5)) = 5.56 * 10^(-10)\\\\(x^(2))/(0.0750 - x) = 5.56 * 10^(10)\\\\\text{Check for negligibility of }x\\(0.0750)/(5.56 * 10^(-10)) = 1.3 * 10^(6) > 400\\\\\therefore x \text{ $\ll$ 0.0750}`

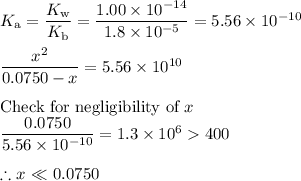
`(x^(2))/(0.0750) = 5.56 * 10^(-10)\\\\x^(2) = 0.0750 * 5.56 * 10^(-10)\\x^(2) = 4.17 * 10^(-11)\\x = \sqrt{4.17 * 10^(-11)}\\\rm [H_(3)O^(+)] =x = 6.46 * 10^(-6)\, mol \cdot L^(-1)`

(iv) Calculate the pH

`\text{pH} = -\log{\rm[H_(3)O^(+)]} = -\log{6.46 * 10^(-6)} = \large \boxed{\mathbf{5.19}}`

The titration curve below shows the pH at the beginning and at the equivalence point of the titration.