Question

A golf pro swings a golf club, striking a golf ball that has a mass of 55.0 g. The club is in contact with the ball for only 0.00340 s. After the collision, the ball leaves the club at a speed of 46.0 m/s. What is the magnitude of the average force (in N) exerted on the ball by the club?

Answer 1

To solve this problem it is necessary to apply the concepts related to Newton's second law and the equations of motion description for acceleration.

From the perspective of acceleration we have to describe it as

`a = (\Delta v)/(\Delta t)`

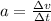
Where,

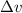`\Delta v` = Velocity

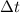`\Delta t`= time

At the same time by the Newton's second law we have that

F = ma

Where,

m = mass

a = Acceleration

Replacing the value of acceleration we have

`F = m ((\Delta v)/(\Delta t))`

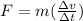
Our values are given as,

`m = 55*10^(-3)Kg`

`v = 46m/s`

`t = 0.00340s`

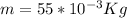
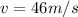
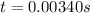
Replacing we have,

`F = m ((\Delta v)/(\Delta t))`

`F = (55*10^(-3))((46)/(0.00340))`

`F = 744.11N`

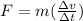
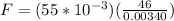
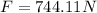
Therefore the magnitude of the average force exerted on the ball by the club is 744.11N