Question

A square has side length (x+5) units. What is it’s area

Answer 1

The area of square is
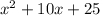`x^(2)+10 x+25` square units

Solution:

Given that square has side length (x+5) units

To find: area of square

The area of square is given as:

`\text {Area of square }=\mathrm{a}^(2)`

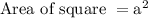
Where "a" is the length of side

From question, length of each side "a" = x + 5 units

Substituting the value in above formula,

`\text {Area of square }=(x+5)^(2)`

`{\text {Expanding }(x+5)^(2) \text { using the algebraic identity: }} \\\\ {(a+b)^(2)=a^(2)+2 a b+b^(2)}\end{array}`

`\begin{array}{l}{\text {Area of square }=x^(2)+2(x)(5)+5^(2)} \\\\ {\text {Area of square }=x^(2)+10 x+25}\end{array}`

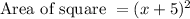
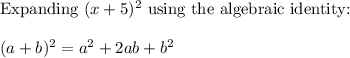
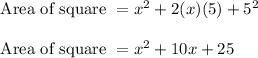
Thus the area of square is
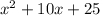`x^(2)+10 x+25` square units