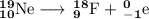Question

Write a balanced equation for each of the following nuclear reactions: (a) mercury-180 decays into platinum-176 (b) zirconium-90 and an electron are produced by the decay of an unstable nucleus (c) thorium-232 decays and produces an alpha particle and a radium-228 nucleus, which decays into actinium-228 by beta decay (d) neon-19 decays into fluorine-19

Answer 1

`\rm (a)\quad _(80)^(180)\text{Hg} \longrightarrow \,  _(78)^(176)\text{Pt}  + \, _(2)^(4)\text{He}\\\\(b) \quad _(39)^(90)\text{Y} \longrightarrow \, _(40)^(90)\text{Zr}  + \, _(-1)^(0)\text{e}\\\\(c) \quad _(90)^(232)\text{Th} \longrightarrow \, _(88)^(228)\text{Ra}  + \, _(2)^(4)\text{He}\\\\. \qquad _(88)^(228)\text{Ra} \longrightarrow \, _(89)^(228)\text{Ac}  +\, _(-1)^(0)\text{e}\\\\(d) \quad _(10)^(19)\text{Ne} \longrightarrow \, _(9)^(18)\text{F}  + \, _(-1)^(0)\text{e}`

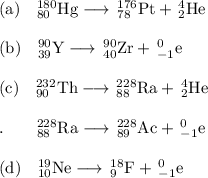
Step-by-step explanation:

(a) Hg-180 to Pt-176

The unbalanced nuclear equation is

`_(80)^(180)\text{Hg} \longrightarrow \, _(78)^(176)\text{Pt} \,  + \, ?`

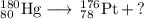
It is convenient to replace the question mark by an atomic symbol,
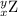`_(x)^(y)\text{Z}`, where x = the atomic number, y = the mass number, and Z = the symbol of the element .

Then your equation becomes

`_(80)^(180)\text{Hg} \longrightarrow \, _(78)^(176)\text{Pt}  + \, _(x)^(y)\text{Z}`

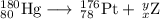
The main point to remember in balancing nuclear equations is that the sums of the superscripts and the sums of the subscripts must be the same on each side of the equation.

Then

80 = 78 + x, so x = 2

180 = 176 + y, so y =180 - 176 = 4

Element 2 is helium, so the nuclear equation becomes

`\bf _(80)^(180)\text{Hg} \longrightarrow \,  _(78)^(176)\text{Pt}  + \, _(2)^(4)\text{He}`

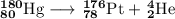
A helium nucleus is also called an alpha particle, so this reaction is an example of alpha decay.

(b) Production of Zr-90 and an electron

`_(x)^(y)\text{Z} \longrightarrow \, _(40)^(90)\text{Zr}  +\, _(-1)^(0)\text{e}`

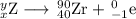
x = 40 - 1 = 39

y = 90 + 0 = 90

The balanced nuclear equation is

`\bf_(39)^(90)\text{Y} \longrightarrow \, _(40)^(90)\text{Zr}  + \, _(-1)^(0)\text{e}`

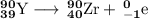
(c) Th-232 to Ra-228 to Ac-228

`\bf _(90)^(232)\text{Th} \longrightarrow \, _(88)^(228)\text{Ra}  + \, _(2)^(4)\text{He}\\\\_(88)^(228)\text{Ra} \longrightarrow \, _(89)^(228)\text{Ac}  +\, _(-1)^(0)\text{e}`

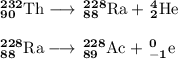
(d) Ne-19 to F-19

`_(10)^(19)\text{Ne} \longrightarrow \, _(9)^(18)\text{F}  + \, _(x)^(y)\text{Z}`

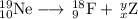
10 = 9 + x, so x = 1

19 = 18 + y , so y = -1

The balanced nuclear equation is

`\bf _(10)^(19)\text{Ne} \longrightarrow \, _(9)^(18)\text{F}  + \, _(-1)^(0)\text{e}`